Topic outline

  • KAPITA SELEKTA MATEMATIKA TINGKAT DASAR

    Dosen Pengampu

      Nama : RIRIN WIDIYASARI
    Email: ririn.widiyasari@umj.ac.id
    Mata Kuliah   :   KAPITA SELEKTA MATEMATIKA TINGKAT DASAR
    Kode   :   WP08031203
    Program Studi   :   S1 Pendidikan Matematika
    Perguruan Tinggi   :   Universitas Muhammadiyah Jakarta

    Deskripsi Singkat Mata Kuliah:

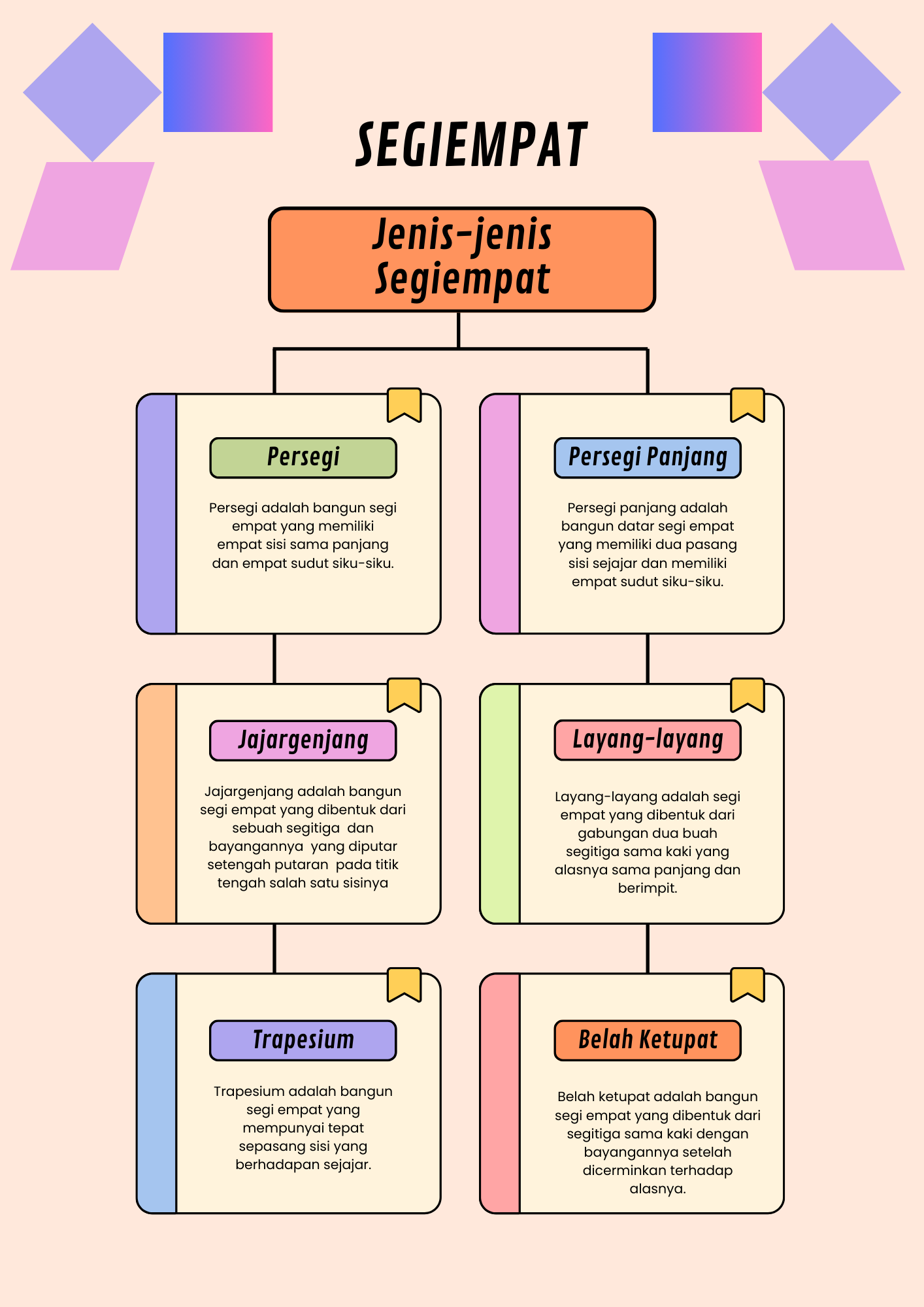
    Mata kuliah ini memberikan penguatan substansi matematika baik di sekolah dasar dan menengah kepada mahasiswa. Mahasiswa dapat mengidentifikasi, mengembangkan, menguasai dan mengaplikasikan materi yang esensial di matematika. Materi secara berurutan mencakup beberapa pokok bahasan, yaitu sebelum ujian tengah semester adalah Segitiga, Segi Empat, Lingkaran, Garis Singgung Lingkaran, dan sesudah ujian tengah semester adalah Bangun Ruang (Sisi Datar dan Sisi Lengkung), Barisan dan Deret, Bilangan Bulat dan Aritmatika Sosial.

    Assalamualaikum Wr.. Wb...

    Perkenalkan saya Ririn Widiyasari dosen pengampu mata kuliah kapita selekta matematika tingkat dasar yang akan mengampu mata kuliah ini selama satu semester. Mari belajar dan diskusi bersama semoga perkuliahan berjalan dengan baik dan lancar..

    Selamat datang teman-teman mahasiswa hebat salam kenal ya, pada halaman pembelajaran daring ini, semoga kita semua mendapatkan rahmat dan hidayah dari Allah SWT sehingga perjuangan teman-teman dalam menuntut ilmu memperoleh manfaat bagi diri kita.. Semangat belajarnya ya teman-teman... 

    Pertama, teman-teman bisa buka rps dan kontrak kuliah yaa.. 

    Syarat absensi adalah mengikuti seluruh pembelajaran dari membaca flip book, mempelajari ppt, dan aktif melakukan diskusi serta mengumpulkan tugas tepat waktu ya..

     

      Unduh RPS

  • Pertemuan ke 1: Segitiga

    Perkuliahan Kamis 03 Oktober 2024 Pukul 16.00 - 17.40 
    Assalamualaikum wr wb.. Teman-teman mahasiswa baca terlebih dahulu Sub CPMK dan Indikatornya yaa... Kita akan mempelajari materi segitiga didalamnya terdiri dari sifat-sifat segitiga, keliling dan luas segitiga serta permasalahan menngenai materi segitiga dalam kehidupan sehari-hari.
    Sub CPMK1: 
    Mahasiswa dapat mengidentifikasi sifat-sifat, keliling dan luas serta permasalahan mengenai materi segitiga dan mengaplikasikan konsep matematika pada segitiga.
    Indikator:
    1. Ketepatan mahasiswa dalam mengidentifikasi dan mengembangkan  mengenai sifat-sifat dan unsur-unsur segitiga, jenis-jenis segitiga, melukis segitiga, garis tinggi, garis bagi, dan garis berat serta garis sumbu.
    2. Ketepatan mahasiswa dalam memahami keliling segitiga, luas segitiga, dan menyelesaikan permasalahan yang berkaitan dengan keliling dan luas segitiga.
    3. Ketepatan mahasiswa dalam menganalisis dan mengaplikasikan konsep matematika pada segitiga.
    Materi:

    Pengertian dan sifat-sifat segitiga.

    Luas dan Keliling segitiga.

    Permasalahan dan solusi menyelesaikan masalah segitiga.

    Aplikasi konsep matematika pada segitiga.

    Metode Pembelajaran: Case Method, Project Based Learning dan diskusi

    Kriteria Penilaian:

    Teknik Tes: Penugasan dan Latihan Soal 

    Bentuk non-test: Partisipasi dan kehadiran serta keaktifan di kelas

  • Pertemuan ke 2: Segiempat

    Assalamualaikum teman-teman mahasiswa jumpa kembali di materi segiempat, mari kita belajar bersama dan berdiskusi bersama ya.. Sebelumnya pelajari dulu Sub CPMK dan indikatornya yaa..

    Sub CPMK 2:

    Mahasiswa dapat mengidentifikasi sifat-sifat, keliling dan luas serta permasalahan mengenai materi bangun datar segi empat.

    Indikator: 

    1. Ketepatan mahasiswa dalam mengidentifikasi mengenai unsur-unsur bangun datar segiempat, sifat-sifat segiempat.

    2. Ketepatan mahasiswa dalam menyelesaikan permasalahan mengenai keliling dan luas segiempat.

    Materi:

    Pengertian dan sifat-sifat bangun datar segiempat.

    Keliling dan luas bangun datar segiempat (persegi, persegi panjang, jajar genjang, layang-layang, belah ketupat, trapesium).

    Permasalahan dan solusi menyelesaikan masalah bangun datar segiempat.

    Metode Pembelajaran:

    Case Method,

    Project Based Learning dan diskusi

    Kriteria Penilaian:

    Teknik Tes:

    - Penugasan

    - Latihan Soal

     Bentuk non-test:

    - Partisipasi dan kehadiran

    - Keaktifan

  • Pertemuan ke 3: Segiempat (Bag.2)

    Assalamualaikum teman-teman mahasiswa jumpa kembali di materi segiempat, mari kita belajar bersama dan berdiskusi bersama ya.. Sebelumnya pelajari dulu Sub CPMK dan indikatornya yaa.. Kali ini segiempat bagian ke-2

    Sub CPMK 2:

    Mahasiswa mampu menganalisis dan mengaplikasikan konsep matematika pada materi segi empat.

    Indikator:

    Ketepatan mahasiswa dalam menganalisis dan mengaplikasikan konsep matematika pada materi segiempat.

    Materi:

    Aplikasi konsep matematika pada segiempat.

    Metode Pembelajaran:

    Case Method,

    Project Based Learning dan diskusi

    Kriteria Penilaian: 

    Teknik Tes:

    -       Penugasan

    -       Latihan Soal

    Bentuk non-test:

    -       Partisipasi dan kehadiran

    -       Keaktifan

  • Pertemuan ke 4: Lingkaran

    Assalamualaikum teman-teman mahasiswa jumpa kembali di materi lingkaran, mari kita belajar bersama dan berdiskusi bersama ya.. Sebelumnya pelajari dulu Sub CPMK dan indikatornya yaa..

    Sub CPMK 3:

    Mahasiswa dapat mengidentifikasi unsur-unsur lingkaran, memahami keliling dan luas lingkaran.

    Indikator:

    1. Ketepatan mahasiswa dalam mengidentifikasi mengenai unsur-unsur lingkaran, busur, juring, tembereng, sudut-sudut pada bidang lingkaran.

    2. Ketepatan mahasiswa dalam menyelesaikan permasalahan mengenai keliling dan luas  lingkaran.

    Materi:

    Pengertian dan unsur-unsur lingkaran, keliling dan luas lingkaran.

    Permasalahan dan penyelesaian permasalahan lingkaran.

    Metode Pembelajaran:

    Case Method,

    Project Based Learning dan diskusi

    Kriteria Penilaian:

    Teknik Tes:

    -       Penugasan

    -       Latihan Soal

    Bentuk non-test:

    -       Partisipasi dan kehadiran

    -       Keaktifan

  • Pertemuan ke 5: Lingkaran (Bag.2)

    Assalamualaikum teman-teman mahasiswa jumpa kembali di materi lingkaran, mari kita belajar bersama dan berdiskusi bersama ya.. Sebelumnya pelajari dulu Sub CPMK dan indikatornya yaa.. Kali ini lingkaran bagian ke-2

    Sub CPMK 3:

    Mahasiswa mampu menganalisis dan mengaplikasikan konsep matematika pada  lingkaran.

    Indikator:

    3. Ketepatan mahasiswa dalam menganalisis dan mengaplikasikan konsep matematika pada lingkaran.

    Materi:

    Aplikasi konsep matematika pada materi lingkaran.

    Metode Pembelajaran:

    Case Method,

    Project Based Learning dan diskusi

    Teknik Tes:

    -       Penugasan

    -       Latihan Soal

    Bentuk non-test:

    -       Partisipasi dan kehadiran

    -       Keaktifan

  • Pertemuan ke 6: Garis Singgung Lingkaran

    Assalamualaikum teman-teman mari kita belajar mengenai materi garis singgung lingkaran, materi ini terdiri dari unsur-unsur garis singgung lingkaran, cara melukis garis singgung lingkaran dan cara menyelesaikan masalah dalam kehidupan sehari-hari yang berkaitan dengan garis singgung lingkaran...

    Sub CPMK4:

    Mahasiswa dapat mengidentifikasi unsur-unsur garis singgung lingkaran, serta menyelesaikan permasalahan mengenai garis singgung lingkaran.

    Indikator:

    1. Ketepatan mahasiswa dalam mengidentifikasi mengenai unsur-unsur garis singgung dua lingkaran, lingkaran luar dan lingkaran dalam.

    2. Ketepatan mahasiswa dalam menentukan solusi terhadap permasalahan mengenai garis singgung lingkaran.

    Materi:

    Pengertian dan unsur-unsur garis singgung lingkaran.

    Permasalahan dan penyelesaian masalah garis singgung lingkaran.

    Metode Pembelajaran: Case Method, Project Based Learning dan diskusi

    Teknik Tes: Penugasan dan Latihan Soal

    Bentuk non-test: Partisipasi dan kehadiran serta keaktifan

  • Pertemuan ke 8: UTS

    UTS --> Via CBT

    Materi: 

    Segitiga

    Segiempat

    Lingkaran

    Garis Singgung Lingkaran

    • UTS Quiz

      Silahkan kerjakan soal berikut ini dengan teliti dan hati-hati..

  • Pertemuan ke 9: Bangun Ruang (Sisi Datar)

    Assalamualaikum Para Mahasiswa Hebat semuanya...

    Kali ini kita akan memasuki Sub CPMK 5 dimana teman-teman akan mempelajari unsur-unsur dari bangun ruang sisi datar yang terdiri dari kubus, balok, prisma dan limas. Teman-teman juga akan mempelajari jaring-jaring dari masing-masing bangun ruang sisi datar tersebut termasuk jaring-jaring kubus, jaring-jaring balok, jaring-jaring prisma dan jaring-jaring limas. Selanjutnya teman-teman akan belajar menyelesaikan permasalahan yang berkaitan dengan luas permukaan dan volume bangun ruang termasuk permasalahan nyata atau permasalahan dalam kehidupan sehari-hari.. Selengkapnya kita simak materi di bawah ini yaaa...

    Sub CPMK 5:

    Mahasiswa mampu mengidentifikasi unsur-unsur, jaring-jaring, luas permukaan bangun ruang, dan volume bangun ruang serta memahami permasalahan mengenai luas dan volume bangun ruang.

    Indikator:

    Ketepatan mahasiswa dalam mengidentifikasi mengenai unsur-unsur bangun ruang sisi datar dengan bidang banyak, jaring-jaring bangun ruang, luas permukaan dan volume bangun ruang sisi datar.

    Materi:

    Sumber belajar yang bisa dipelajari yaitu unsur-unsur bangun ruang sisi datar, bangun ruang dengan bidang banyak, jaring-jaring bangun ruang, luas permukaan bangun ruang dan volume bangun ruang (bangun ruang sisi datar yang terdiri dari kubus, balok, prisma dan limas).

    Metode Pembelajaran:

    Case Method,

    Project Based Learning dan diskusi

    Teknik Tes: Penugasan dan Latihan Soal

    Bentuk non-test: Partisipasi dan kehadiran serta keaktifan selama di forum diskusi.

  • Pertemuan ke 10: Bangun Ruang (Sisi Lengkung)

    Assalamualaikum wr. wb. Teman-teman mahasiswa hebat, kita akan melanjutkan pembahasan pada pertemuan sebelumnya dimana teman-teman sekarang akan mempelajari unsur-unsur dari bangun ruang sisi lengkung yang terdiri dari Kerucut, Tabung, dan Bola. Teman-teman juga akan mempelajari jaring-jaring dari masing-masing bangun ruang sisi lengkung tersebut termasuk jaring-jaring Kerucut, jaring-jaring Tabung, dan jaring-jaring Bola. Selanjutnya teman-teman akan diberikan case methods dan tugas individu untuk menyelesaikan permasalahan yang berkaitan dengan luas permukaan dan volume bangun ruang sisi lengkunh termasuk permasalahan nyata atau permasalahan dalam kehidupan sehari-hari.. Namun sebelumnya teman-teman bisa mengulang kembali materi dari pertemuan sebelumnya.. Selengkapnya kita simak materi di bawah ini yaaa...

    Sub CPMK 5:

    Mahasiswa mampu mengidentifikasi unsur-unsur, jaring-jaring, keliling, dan luas bangun ruang serta memahami permasalahan mengenai luas dan volume bangun ruang.

    Indikator:

    Ketepatan mahasiswa dalam mengidentifikasi mengenai unsur-unsur bangun ruang sisi lengkung, jaring-jaring bangun ruang, luas permukaan dan volume bangun ruang sisi lengkung.

    Materi:

    Sumber belajar yang bisa dipelajari yaitu unsur-unsur bangun ruang sisi lengkung,  jaring-jaring bangun ruang, luas permukaan bangun ruang dan volume bangun ruang (sisi lengkung).

    Metode Pembelajaran:

    Case Method,

    Project Based Learning dan diskusi

    Kriteria Penilaian:

    Teknik Tes: Penugasan Case Method dan Latihan Soal (Tugas Individu)

    Bentuk non-test:

    Partisipasi (Isi Forum Diskusi) dan kehadiran serta Keaktifan

  • Pertemuan ke 11: Aplikasi Bangun Ruang (Bag 3)

    Sub CPMK 5:

    Mahasiswa mampu menyelesaikan permasalahan mengenai luas permukaan dan volume bangun ruang, dan mengaplikasikan konsep matematika pada bangun ruang.

    Indikator:

    1. Ketepatan mahasiswa dalam menyelesaikan permasalahan mengenai luas permukaan dan volume bangun ruang.

    2. Ketepatan mahasiswa dalam mengaplikasikan konsep matematika pada materi bangun ruang.

    Materi:

    Luas permukaan bangun ruang, volume bangun ruang (bangun ruang sisi datar dan sisi lengkung).

    Aplikasi konsep matematika pada bangun ruang (sisi datar dan sisi lengkung).

    Metode Pembelajaran:

    Case Method,

    Project Based Learning dan diskusi

    Kriteria Penilaian:

    Teknik Tes:

    -       Penugasan Project Based Learning

    -       Latihan Soal

    Bentuk non-test:

    -       Partisipasi dan kehadiran

    -       Keaktifan

  • Pertemuan ke 12: Barisan dan Deret

    Sub CPMK 6:

    Mahasiswa mampu mengidentifikasi dan memahami pola bilangan barisan dan deret dan menyelesaikan permasalahan mengenai materi barisan dan deret.

    Indikator:

    1. Ketepatan mahasiswa dalam mengidentifikasi mengenai pola bilangan, barisan aritmatika, barisan geometri, deret aritmatika, deret geometri.

    2. Ketepatan mahasiswa dalam menyelesaikan permasalahan mengenai materi barisan dan deret.

    Materi:

    Materi barisan dan deret pola bilangan, barisan aritmatika, barisan geometri, deret aritmatika, deret geometri.

    Permasalahan barisan dan deret dalam kehidupan sehari-hari.

    Metode Pembelajaran:

    Case Method,

    Project Based Learning dan diskusi

    Kriteria Penilaian:

    Teknik Tes:

    -  Penugasan

    -  Latihan Soal

    Bentuk non-test:

    -  Partisipasi dan kehadiran

    -  Keaktifan

  • Pertemuan ke 13: Aplikasi Barisan dan Deret

    Sub CPMK 6:

    Mahasiswa mampu mengaplikasikan konsep matematika pada materi barisan dan deret.

    Indikator:

    Ketepatan mahasiswa dalam mengaplikasikan konsep matematika pada materi barisan dan deret.

    Materi:

    Aplikasi barisan dan deret.

    Aplikasi konsep matematika barisan dan deret.

    Metode Pembelajaran:

    Case Method,

    Project Based Learning dan diskusi

    Kriteria Penilaian:

    Teknik Tes:

    -       Penugasan

    -       Latihan Soal

    Bentuk non-test:

    -       Partisipasi dan kehadiran

    -       Keaktifan

    • Pertemuan ke 14: Bilangan Bulat

      Sub CPMK 7:

      Mahasiswa mampu mengidentifikasi sifat operasi hitung bilangan bulat, serta permasalahan mengenai materi bilangan bulat serta menguasai dan mengaplikasikan konsep matematika pada materi bilangan bulat.

      Indikator:

      1. Mahasiswa mampu mengidentifikasi mengenai sifat operasi hitung bilangan, bilangan bulat, operasi hitung bilangan bulat, dan sifat-sifat operasi hitung bilangan bulat. 

      2. Mahasiswa mampu menyelesaikan masalah mengenai pemangkatan dan penarikan akar bilangan bulat, operasi hitung bilangan berpangkat, dan pola bilangan bulat.

      3. Mahasiswa mampu dalam melakukan operasi hitung pada bilangan bulat, bilangan rasional, bilangan desimal, bilangan berpangkat dan bilangan berpangkat tak sebenarnya dengan beberapa cara dan menggunakannya dalam menyelesaikan masalah.

      4. Mahasiswa mampu mengaplikasikan konsep matematika yang berkaitan dengan operasi hitung bilangan, bilangan bulat, dan bilangan berpangkat.

      Materi:

      Materi bilangan bulat, bilangan rasional, bilangan desimal, bilangan berpangkat dan bilangan berpangkat tak sebenarnya.

      Bilangan dengan menggunakan notasi ilmiah.

      operasi aritmatika pada ragam bilangan bulat, bilangan rasional, bilangan desimal, bilangan berpangkat dan bilangan berpangkat tak sebenarnya.

      operasi hitung pada bilangan bulat, bilangan rasional, bilangan desimal, bilangan berpangkat dan bilangan berpangkat tak sebenarnya dengan beberapa cara dan menggunakannya dalam menyelesaikan masalah.

      Metode Pembelajaran:

      Case Method,

      Project Based Learning dan diskusi

      Kriteria Penilaian:

      Teknik Tes:

      - Penugasan

      - Latihan Soal

      Bentuk non-test:

      - Partisipasi dan kehadiran

      - Keaktifan

    • Pertemuan ke 15: Aritmatika Sosial

      Sub CPMK 8:

      Mahasiswa mampu mengidentifikasi dan menyelesaikan permasalahan mengenai materi perbandingan dan aritmatika sosial serta  mengaplikasikan konsep matematika pada materi perbandingan dan aritmatika sosial.

      Indikator:

      1. Mahasiswa mampu mengidentifikasi mengenai materi perbandingan (perbandingan senilai, perbandingan berbalik nilai, perbandingan skala) dan aritmatika sosial (nilai keseluruhan, nilai per unit, nilai sebagian, harga penjualan, harga pembelian, untung, rugi, diskon, bruto, neto, tara, pajak, bunga tunggal dan bunga majemuk).

      2. Mahasiswa mampu dalam menentukan solusi terhadap permasalahan mengenai perbandingan dan aritmatika sosial.

      3. Mahasiswa mampu dalam mengaplikasikan konsep matematika pada materi perbandingan dan aritmatika sosial.

      Materi:

      Materi perbandingan (perbandingan senilai, perbandingan berbalik nilai, perbandingan skala)

      Materi aritmatika sosial,  nilai keseluruhan, nilai per unit, nilai sebagian, harga penjualan, harga pembelian, untung, rugi, diskon, bruto, neto, tara, pajak, bunga tunggal dan bunga majemuk.

      Aplikasi konsep matematika pada aritmatika sosial dalam kehidupan sehari-hari.

      Metode Pembelajaran:

      Case Method,

      Project Based Learning dan diskusi

      Kriteria Penilaian:

      Teknik Tes:

      - Penugasan

      - Latihan Soal

      Bentuk non-test:

      - Partisipasi dan kehadiran

      - Keaktifan

      • Flipbook Artimatika Sosial

      • Berikut Slide PPT Perbandingan dan Aritmatika Sosial:

    • Pertemuan ke 16: UAS

      UAS --> CBT

      Materi:

      Bangun Ruang (Sisi Datar dan Sisi Lengkung)

      Barisan dan Deret

      Bilangan Bulat

      Perbandingan dan Aritmatika Sosial

      • Quiz - Kapita Selekta Matematika Tingkat Dasar

        Kerjakan Quiz di bawah ini dengan jujur.

        Sebelum mengerjakan ucapkan:

        "Saya berjanji demi Allah mengerjakan soal quiz ini dengan jujur tanpa meminta bantuan siapapun termasuk AI dan oranglain."