Topic outline

• Komputasi Numerik

  Collapse all Expand all

  

  Video Pembukaan Mata Kuliah Komputasi Numerik

  Assalamualaikum.. Selamat datang dalam Mata Kuliah Komputasi Numerik. Mata kuliah komputasi numerik ini yang memberi kesempatan kepada mahasiswa untuk dapat menyelesaikan permasalahan matematika secara numerik. Dalam mata kuliah ini akan dibagi menjadi 9 BAB, yaitu Pengenalan Matlab, Error Perhitungan Numerik, Penyelesaian Persamaan Non Linear, Penyelesaian Persamaan Differensial Biasa, dan Penyelesaian Sistem Persamaan Linear dan sampai bab 9. Ada beberapa evaluasi juga dalam mata kuliah ini di antaranya adalah tugas, ujian tengah semester, dan ujian akhir semester. Semoga kita semua diberikan sehat dan semangat selalu untuk belajar ya..

  

  • 

    A. Profil Mata Kuliah Page

    Baik...Berikut ini merupakan Profil Mata Kuliah Komputasi Numerik. Dengan mengetahui Profil Mata Kuliah, anda dapat memiliki informasi dan gambar topik-topik apa saja yang akan dipelajari nantinya ya... Klik link "A. Profil Mata Kuliah" untuk melihat informasi tersebut. Terimakasih semua...
    

  • 

    B. Profil Dosen Pengampu Page

    Di dalam halaman ini, anda dapat mengetahui biodata dosen pengampu secara lengkap. Karena ada pepatah yang mengatakan bahwasanya "Tak kenal, maka tak sayang" (Klik link " B. Profil Dosen Pengampu" untuk melihat Biodata Dosen). Terimakasih semua...
    

  • 

    C. Deskripsi Mata Kuliah Page

    Untuk point ini, anda dapat mengetahui Deskripsi Mata Kuliah Komputasi Numerik, diantaranya tujuan dari perkuliahan, topik-topik yang diberikan, serta pelaksanaan ujian sebagai evaluasi perkuliahan ini. Untuk mengetahu informasi tersebut klik link berikut "C. Deskripsi Mata Kuliah". Terimakasih...

  • 

    D. Capaian Pembelajaran dan RPS Page

    Setelah mengetahui Profil Mata Kuliah, Profil Dosen Pengampu, dan Deskripsi Mata Kuliah, tiba saatnya anda untuk mengetahui Capaian Pembelajaran, sekaligus Peta Kompetensi. Berikut dijelaskan Capaian Pembelajaran Mata Kuliah Komputasi Numerik. KliK Link " D. Capaian Pembelajaran"  dan RPS Mata Kuliah untuk membukanya ya...

  • 

    E. DAFTAR REFERENSI Page

    Berikut merupakan referensi pada mata Komputasi Numerik.

    1. Chapra, S.C., Canale, R.P., ”Numerical Methods for Engineers 6th Ed”, McGrawHill, 2010
    2. Hariadi, V., ”Bahan Ajar Komputasi Numerik”, 2014
    3. Karris, S.T., ”Numerical Analysis Using MATLAB and Spreadsheets 3rd Ed”, Orcards Publications, 2007
    4. Munif, A., Prastyoko, A., ”Penguasaan dan Penggunaan Metode Numerik”, Guna Widya, 1995

  • 

    Aplikasi Android Take a Numeric Page

    

    Baik, sebelum masuk perkuliah, silahkan instal aplikasi android "Take a Numeric" sebagai bahan ajar pendamping pada mata kuliah Komputasi Numeric. Di dalamnya berisi materi-materi terkait komputasi numeric dan contoh coding dari proses komputasi menggunakan Matlab dan juga Python pada berbagai bidang. code tersebut dapat dipraktekkan pada aplikasi Matlab dan Google Colab, Karena hasil akhir perkuliahan ini berupa Tugas Proyek. Klik link berikut untuk mendownload aplikasi: Take a Numeric. Aplikasi ini aman dari scamming atau hal-hal lain yang merugikan pihak pengguna. Terimakasih atas kerjasamanya. salam

  • 

    Announcements Forum

• BAB 1 PENGENALAN MATLAB

  
  

  Assalamualaikum wr wb semua.. Salam hangat.. Bagaimana kabar kalian? nah.. kali ini kita masuk pada bab 1 yaitu Pengenalan Matlab. Matlab adalah singkatan dari Matrix Laboratory (Laboratorium Matriks) dan merupakan bahasa pemrograman yang dibuat dengan tujuan sebagai alat bantu perhitungan yang rumit atau simulasi dari suatu sistem yang ingin di simulasikan. Jangan lupa instal aplikasi atau softwarenya di komputer/laptop kalian. Untuk materi lebih lengkap silahkan simak video penjelasan  di bawah ini. Terimakasih.. Tetap semangat

  
  

  
  

  Video Pengenalan Matlab Mata Kuliah Komputasi Numerik

  
  

  MATLAB adalah salah satu platform yang paling banyak digunakan untuk mengolah angka dan bahasa pemrograman. Menurut MathWokrs, MATLAB adalah platform pemrograman yang menggunakan bahasa berbasis matriks sehingga umumnya digunakan untuk menganalisis data, membuat algoritma, serta menciptakan pemodelan dan aplikasi. Untuk materi lebih lengkap terkait kegunaan dan sistem pada MATLAB bisa klik pada sub bab di bawah ini
  

  • 

    1.1 Fungsi MATLAB Page

    Menurut Dummies, berikut adalah 5 fungsi MATLAB yang sering digunakan. Untuk lebih jelasnya silahkan klik 1.1 Fungsi MATLAB ya.

  • 

    1.2 Sistem MATLAB Page

    MATLAB terdiri dari 5 bagian sistem diantaranya MATLAB languange, working environment, dan lainnya. Untuk selengkapnya klik 1.2 Sistem MATLAB.

  • 

    1.3 Fasilitas MATLAB Page

    Ada 4 fasilitas MATLAB diantaranya Current Directory, Workspace atau pencari tempat kerja dan lainnya. Untuk selengkapnya silahkan klik 1.3 Fasilitas MATLAB.

  • 

    1.4 Matematika Sederhana pada MATLAB Page

    Seperti sebuah kalkulator, MATLAB mengerjakan matematika sederhana. Untuk lebih jelasnya silahkan klik pada sub bab 1.4 Matematika Sederhana pada MATLAB.
    

  • 

    PPT BAB 1 Pengenalan Matlab File

    File ini berisikan Pengenalan Matlab, dimana di dalamnya berisi tentang fasilitas-fasilitas Matlab beserta penjelasannya. Untuk men-download bisa klik PPT BAB 1 Pengenalan Matlab. Terimakasih..

  • 

    Upload Tugas Praktik Pengenalan Matlab Assignment

    Silahkan kerjakan code latihan PPT pada matlab online ya. Kalian dapat meng-upload tugas dalam format rar disini ya.. Waktu pengumpulan tanggal dimulai tanggal 07 Oktober sampai dengan 15 Oktober 2024 Jam 23.00. Maksimal ukuran 10 mb. Terimakasih.

  • 

    Forum Diskusi BAB 1 Pengenalan Matlab

    Jika ada yang perlu didiskusikan mengenai BAB 1 Pengenalan Matlab atau hal lain, bisa kita ngobrol disini ya.. Terimakasih..

• BAB 2 ERROR PERHITUNGAN NUMERIK

  
  

  Assalamualaikum wr wb.. Nah, pada kali ini kalian akan diberikan materi mengenai Error Perhitungan Numerik. kalian dapat mendownload materi dan langsung mempraktikannya pada Matlab editor dengan membuat permasalahan versi kalian dan mengacu pada contoh yang telah diberikan. Untuk mendapatkan hasil maksimal kalian bisa merekam semua kegiatan praktik pada matlab menggunakan screen recording dan dapat diupload di laman youtube atau situs sejenis. Jika ada yang mau didiskusikan dapat menggunakan forum di bawah ini. Namun sebelum melangkah lebih jauh, alangkah baiknya simak dulu penjelasan terkait galat atau error pada video di bawah ini. Terimakasih.. Salam hangat..

  
  

  
  

  Video Penjelasan Terkait Galat/Error

  
  

  Metode numerik adalah teknik penyelesaian permasalahan yang diformulasikan secara matematis dengan cara operasi hitungan. Dalam metode numerik ini dilakukan operasi hitungan dalam jumlah yang banyak dan prosesnya berulang. Sehingga dalam prakteknya perlu bantuan komputer untuk menyelesaikan hitungan tersebut. Galat atau biasa disebut error dalam metode numerik adalah selisih yang ditimbulkan antara nilai sebenarnya dengan nilai yang dihasilkan dengan metode numerik. Dalam metode numerik, hasil yang diperoleh bukanlah hasil yang sama persis dengan nilai sejatinya. Untuk lebih jelasnya silahkan klik sub bab di bawah ini. Semangat terus ya belajarnya
  

  • 

    2.1 Definisi Galat Page

    Kesalahan (error/galat) adalah besarnya perbedaan atau selisih antara nilai taksiran (hampiran/aproksimasi) dengan nilai sesungguhnya (eksak), kesalahan ini biasa timbul karena proses pengukuran atau penggunaan aproksimasi. Untuk lebih jelasnya bisa klik  2.1 Definisi Galat.

  • 

    2.2 Analisis Galat Page

    Menganalisis galat sangat penting di dalam perhitungan yang menggunakan metode numerik. Galat berasosiasi dengan seberapa dekat solusi hampiran terhadap solusi sejatinya. Semakin kecil galatnya, semakin teliti solusi numerik yang didapatkan. Agar lebih jelas bisa klik 2.2 Analisis Galat.

  • 

    2.3 Nilai Galat Page

    Besarnya kesalahan atas suatu nilai taksiran dapat dinyatakan secara kuantitatif dan kualitatif. Materi lebih lanjut silahkan klik 2.3 Nilai Galat ya..

  • 

    2.4 Macam-macam Galat Page

    Ada 3 macam kesalahan dasar yaitu galat bawaan, pemotongan dan pembulatan. Selengkapnya silahkan klik 2.4 Macam-macam Galat.

  • 

    PPT BAB 2 Error Perhitungan Numerik File

    Untuk materi BAB 2 telah dirangkum dalam PPT, bisa kalian donwload di PPT BAB 2 Error Perhitungan Numerik.

  • 

    Upload Tugas Praktik Error Perhitungan Numerik Assignment

    nah..kalian mengerjakan file pdf pada matlab online ya dan selanjutnya dapat mengumpulkan hasil latihan praktIk disini dalam bentuk rar dengan nama mahasiswa_NIM. Pengumpulan Tugas paling lambat 21 Oktober 2024 jam 17.00. Salam semangat ya..

  • 

    Forum Diskusi BAB 2 Error Perhitungan Numerik

    Jika ada yang kurang dimengerti tentang BAB 2 kalian dapat berdiskusi forum ini. Terimakasih

• BAB 3 PENYELESAIAN PERSAMAAN NON LINEAR

  
  

  Assalamualaikum Wr Wb. Salam hangat untuk kalian semua dan mudah-mudahan dalam keadaan sehat.. Amin. Nah, kali ini kita masuk Bab 3 Penyelesaian Persamaan Non Linear. Dalam penyelesaian persamaan non linear, dapat menggunakan beberapa cara diantaranya: Metode Grafik dan Tabulasi; Metode Bijeksi dan Metode Newton Raphson. Lebih jelaskan kalian akan diberikan Video penjelasan terkait Penyelesaian Persamaan Non Linier dan file materi yang ada pada tagihan tugas di bawah ini. Terimakasih...

  
  

  
  

  
  

  Video Penyelesaian Persamaan Non Linier

  
  

  • 

    3.1 Definisi Persamaan Non Linear Page

    Persamaan nonlinear adalah suatu persamaan yang pangkat variabelnya lebih dari satu atau terdapat suku dari persamaan yang merupakan hasil kali dari dua atau lebih variabel-variabelnya. Selengkapnya klik 3.1 Definisi Persamaan Non Linear.

  • 

    3.2 Metode Newton-Rapshon Page

    Untuk selengkapnya silahkan klik 3.2 Metode Newton-Rapshon.

  • 

    3.3 Program Komputer Metode Newton-Rapshon Page

    Untuk program komputer Metode Newton-Rapshon bisa dipelajari pada saat praktik ya..

  • 

    3.4 Metode Substitusi Page

    Silahkan klik 3.4 Metode Substitusi untuk materi selengkapnya ya
  • 

    3.5 Program Komputer Metode Substitusi Page

    Program komputer Metode Substitusi bisa dipelajari bersama pada saat praktik. Semangat ya

  • 

    PPT BAB 3 Penyelesaian Persamaan Non Linear File

    Rangkuman materi dalam bentuk Power Point bisa didownload disini atau klik PPT BAB 3 Penyelesaian Persamaan Non Linear.

  • 

    Latihan Tugas Praktik Penyelesaian Persamaan Non liniear Assignment

    nah..Materi yang perlu dibuat penyelesaiannya yaitu Membuat soal Persamaan non linear dan solusi, kemudian dicari solusinya menggunakan metode Grafik, Tabulasi, Metode Bijeksi, dan Newton Raphson. Ingat jangan sama dengan contoh ya...Kalian dapat mengumpulkan hasil latihan praktek disini. Materi jg kalian dapat juga disini. Tugas praktek dalam bentuk video, kalian dapat mencantumkan URL Yotubenya disini. durasi video antara 2 sampai 4 menit ya...Salam semangat ya..Waktu terakhir upload tugas pada hari Senin tanggal 28 Oktober 2024 jam 17.00 .

  • 

    Forum Diskusi BAB 3 Penyelesaian Persamaan Non Linear

    Jika ada yang kurang dimengerti tentang bab 3 ini kalian dapat berdiskusi forum ini. Terimakasih

• BAB 4 PENYELESAIAN PERSAMAAN DIFFERENSIAL BIASA

  
  

  Assalamualaikum.. Selamat Pagi.. Kita masuk ke BAB 4 yaitu Persamaan Diferensial Biasa (ordinary differential equation) disingkat PDB adalah suatu persamaan diferensial yang hanya mempunyai satu variabel bebas. Metode penyelesaian yang akan kita pelajari dalam penyelesaian Persamaan Differensial Biasa adalah Metode Euler dan Range-Kutta. Untuk lebih jelasnya kalian dapat melihat penjelasan video di bawah ini ya.. SEMANGAT yaa belajarnya

  
  

  
  

  Video Penyelesaian Persamaan Diferensial Biasa

  • 

    4.1 Metode Euller Page

    Metode Euler adalah Metode hampiran paling sederhana untuk menyelesaikan persamaan differensial biasa, agar lebih jelas silahkan klik 4.1 Metode Euller.

  • 

    4.2 Metode Heun Page

    Metode Heun merupakan salah satu peningkatan dari metode Euler. Silahkan klik 4.2 Metode Heun untuk selengkapnya ya..

  • 

    4.3 Metode Titik Tengah Page

    Metode titik tengah menggunakan setengah step size pada metode Euler untuk melakukan estimasi terhadap integral suatu persamaan diferensial. Selengkapnya bisa klik 4.3 Metode Titik Tengah.

  • 

    4.4 Metode Runge-Kutta Orde 4 Page

    Runge-Kutta orde 4 merupakan metode yang paling populer dalam penyelesaian persamaan diferensial. Selengkapnya bisa klik 4.4 Metode Runge-Kutta Orde 4.

  • 

    4.5 Metode Multistep Linear Page

    Jika metode Runge-Kutta mengalami kesulitan karena terlalu banyak evaluasi fungsi yang digunakan, maka metode multistep linier dikembangkan untuk mengatasi masalah ini. Mengenai algoritmanya bisa klik 4.5 Metode Multistep Linear.

  • 

    Materi BAB 4 Penyelesaian Persamaan Differensial Biasa File

    Materi mengenai Penyelesaian Persamaan Differensial Biasa dapat didownload disini ya..

  • 

    PPT BAB 4 Penyelesaian Persamaan Differensial Biasa File

    Rangkuman materi dalam bentuk PPT bisa didownload disini ya atau klik PPT BAB 4 Penyelesaian Persamaan Differensial Biasa.

  • 

    Tugas Praktik Metode Euler Assignment

    Assalamualaikum wr wb semua.. Silahkan upload hasil praktik kalian disini ya..

    1. Hasil Definisi Euler dalam M File
    2. Hasil Praktik dalam Command Window
    3. Screen Shoot solusi dalam bentuk Grafik

    Semua dokumen dijadikan 1 dalam bentuk File dengan jpg dengan nama_nim. Pengumpulan tugas paling lambat 04 November 2024 jam 17.00 ya...

    Terimakasih semua..

  • 

    Forum Diskusi BAB 4 Penyelesaian Persamaan Differensial Biasa

    Jika ada yang ditanyakan terkait materi Persamaan Differensial Biasa, bisa klik disini ya..

• BAB 5 PENYELESAIAN SISTEM PERSAMAAN LINEAR

  
  

  Suatu persamaan disebut linear apabila digambarkan dalam sistem koordinat kartesius akan membentuk garis lurus. Apabila terdapat lebih dari satu persamaan linear, persamaan tersebut akan menjadi sebuah sistem. Bentuk umum untuk persamaan linear adalah: y = mx + b. Di bawah ini merupakan beberpa metode yang digunakan untuk menyelesaikan Sistem Persamaan Linear.
  

  
  

  
  

  Video Penjelasan Penyelesaian Sistem Persamaan Linier
  

  • 

    5.1 Metode Eliminasi Gauss Page

    Untuk suatu sistem persamaan yang banyak maka persamaan ditulis dapat ditulis dalam bentuk matriks. Metode eliminasi Gauss ini adalah dengan mengeliminasi satu variabel dari satu persamaan dengan persamaan lainnya, Untuk lebih lengkapnya silahkan klik 5.1 Metode Eliminasi Gauss.

  • 

    5.2 Metode Eliminasi Gauss-Jordan Page

    Metode ini adalah variasi dari metdode eliminasi Gauss yang telah diterangkan
    pada Sub Bab sebelumnya. Agar lebih jelas silahkan simak pada 5.2 Metode Eliminasi Gauss-Jordan.
    

  • 

    5.3 Metode Cholesky Page

    Metode ini berlaku untuk hanya untuk matrik [A] tridiagonal saja, yang banyak dijumpai dalam problem khususnya didalam penyelesaian persamaan diferensial orde dua. Untuk materi lebih lengkap silahkan klik 5.3 Metode Cholesky.

  • 

    5.4 Metode Iterasi Page

    Prinsip metode ini adalah dengan melakukan perhitungan variabel yang dicari berulang-ulang sampai konvergen dan akhirnya didapatkan solusi. Selengkapnya bisa klik 5.4 Metode Iterasi.

  • 

    PPT BAB 5 Penyelesaian Sistem Persamaan Linear File

    Rangkuman materi dalam bentuk PPT bisa didownload disini ya atau bisa klik PPT BAB 5 Penyelesaian Sistem Persamaan Linear, jangan lupa dipelajari lagi

  • 

    Tugas BAB 5 Penyelesaian Sistem Persamaan Linier Assignment

    Assalamualaikum wr wb semua.. Silahkan upload hasil praktik kalian disini ya...

    1. Hasil Penyelesaian Sistem Persamaan Linier dalam M FIle
    2. Hasil Praktek dalam Command Window

    Semua dokumen dijadikan 1 dalam bentuk File dengan format rar dengan nama file: nama_nim. Pengumpulan Tugas paling lambat tanggal 11 November 2024 jam 17.00 ya...

    Terimakasih semua... Selamat mengerjakan

  • 

    Forum Diskusi BAB 5 Penyelesaian Sistem Persamaan Linear

    Kalian bisa meninggalkan pesan disini, jika ada yang ingin didiskusikan terkait Sistem Persamaan Linear ya..

• UTS (Ujian Tengah Semester)

  
  

  Setengah perjalanan dari perkulian ini telah kita lewati, maka waktunya evaluasi ya.. Ujian Tengah Semester ini untuk evaluasi BAB 1, BAB 2, BAB 3,  BAB 4 dan BAB 5. Untuk soal silahkan check link di bawah. Semangat!

  • 

    Soal UTS Komputasi Numerik Assignment

    Kerjakan soal di bawah ini dan upload jawaban (bentuk rar) kalian tepat waktu ya dan Selamat mengerjakan

    1. Pada kuliah komputasi numerik akan dibuat bobot penilaian dengan kriteria, presensi 5%, presentasi 15%, tugas 40%, UTS 20% dan UAS 20%. Buatlah input data permasalahan tersebut pada Matlab!
    2. Hitunglah jumlah √1 + √2 + √3 + ⋯ √500 dengan menggunakan pembulatan sampai dua angka desimal. Berapakah maksimum galat penjumlahan tersebut? Berapakah galat yang sesungguhnya?
    3. Gunakan metode grafik untuk menentukan penyelesaian dari y₁= x₁+ 2x₁- 5

    Deadline pengumpulan UTS hari Selasa Tanggal 26 November 2024 jam 17.00. Terimakasih semua

  • 

    Forum Diskusi UTS

    Jika ada yang ditanyakan terkait UTS, klik disini ya..

• BAB 6 PENYELESAIAN KURVA INTERPOLASI

  
  

  
  

  Hallo semoga sehat selalu ya, setelah UTS kita lanjut ke BAB berikutnya yaitu Penyelesaian Kurva Interpolasi. Interpolasi adalah teknik untuk mencari nilai suatu variabel yang hilang di antara dua data atau lebih yang telah diketahui nilainya. Adapun sejumlah manfaat yang didapat dari mempelajari interpolasi, yakni sebagai berikut: Meminimalisir data yang tersaji tidak lengkap atau hilang, Mengetahui adanya outlier atau nilai yang berbeda jauh dengan mayoritas data yang dimiliki, Mencegah data yang telah terkumpul kemudian dihapus kembali karena terjadi kesalahan data. Agar lebih jelas, silahkan simak sub bab-sub bab di bawah ini ya. Sebelum itu simak video penjelasan berikut ini ya.
  

  
  

  
  

  Video Penjelasan Penyelesaian Kurva Interpolasi

  
  

  • 

    6.1 Interpolasi Linear Page

    Interpolasi linier merupakan polinomial tingkat pertama dan melalui suatu garis lurus pada setiap dua titik masukan yang berurutan. Selengkapnya silahkan klik 6.1 Interpolasi Linear.

  • 

    6.2 Interpolasi Kuadrat Page

    Interpolasi kuadratik merupakan metode penyempurna dari interpolasi linier. Selanjutnya silahkan klik 6.2 Interpolasi Kuadrat.

  • 

    6.3 Bentuk Umum Interpolasi Polinomial Page

    Interpolasi polinomial merupakan teknik interpolasi dengan mengasumsikan pola data yang dimiliki mengikuti pola polinomial baik berderajat satu (linier) maupun berderajat tinggi. Untuk Rumusnya silahkan klik 6.3 Bentuk Umum Interpolasi Polinomial.
    

  • 

    PPT BAB 6 Penyelesaian Kurva Interpolasi File

    Silahkan download PPT ini atau klik PPT BAB 6 Penyelesaian Kurva Interpolasi dan jangan lupa dipelajari ya

  • 

    Tugas BAB 6 Penyelesaian Kurva Interpolasi Assignment

    Berikut ini adalah tugas terkait BAB 6 silahkan klik disini, semangat yaa mengerjakannya

  • 

    Forum Diskusi BAB 6 Penyelesaian Kurva Interpolasi

    Jika ada yang ingin ditanyakan terkait bab ini, bisa klik disini ya.

• BAB 7 FUNGSI REGRESI

  
  

  
  

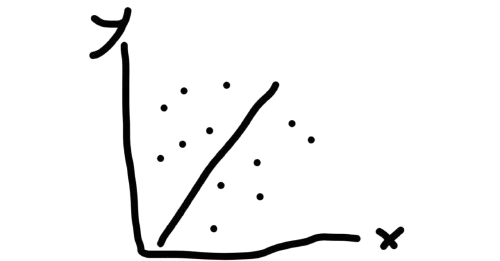
  Dalam BAB ini biasanya akan dibuat kurva atau fungsi berdasarkan sebaran data, kurva yang dibentuk diharapkan dapat mewakili titik-titik pada data. Beberapa sub bab akan dibahas dalam pertemuan kali ini, agar lebih jelas silahkan tonton Video penjelasan dan klik sub bab di bawah ya. Semangat terus ya

  
  

  
  

  Video Penjelasan Terkait Fungsi Regresi

  • 

    7.1 Deviasi Standard Page

    Untuk menentukan deviasi standard dapat dengan mengambil sejumlah data, selengkapnya bisa klik 7.1 Deviasi Standard.

  • 

    7.2 Regresi Linear Page

    Regresi linear adalah teknik analisis data yang memprediksi nilai data yang tidak diketahui dengan menggunakan nilai data lain yang terkait dan diketahui. Untuk materi selanjutnya silahkan klik 7.2 Regresi Linear.

  • 

    7.3 Regresi Polynomial Page

    Regresi polinomial adalah bentuk analisis regresi di mana hubungan antara variabel bebas x dan variabel terikat y dimodelkan sebagai polinomial derajat ke -n dalam x. Selanjutnya silahkan klik 7.3 Regresi Polynomial.

  • 

    PPT BAB 7 Fungsi Regresi File

    Silangkah download PPT BAB 7 disini ya, jangan lupa dipelajari

  • 

    Tugas BAB 7 Fungsi Regresi Assignment

    Silahkan mendownload tugas BAB 7 disini, dan jangan lupa upload hasilnya tepat waktu ya..

  • 

    Forum Diskusi BAB 7 Fungsi Regresi

    Jika ada yang ingin ditanyakan terkait bab ini silahkan klik Forum Diskusi BAB 7 Fungsi Regresi.

• BAB 8 PENYELESAIAN INTEGRASI NUMERIK

  
  

  
  

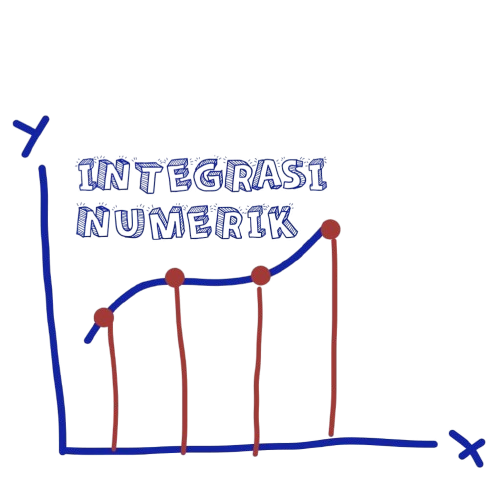
  Integral adalah mencari luasan dibawah suatu kurva dari satu titik ke titik yang lain. Biasanya integral numerik ini dilakukan apabila integral tersebut tidak bisa dilakukan secara analitik. Sekelompok data yang yang apabila dihubungan secara grafik membentuk suatu kurva dimana antara satu titik data ke titik yang lainnya ditarik garis lurus. Akan ada beberapa metode yang digunakan dalam penyelesaianannya, untuk lebih jelasnya silahkan simak video penjelasan dan sub bab-sub bab di bawah ini.

  
  

  Video Penjelasan Penyelesaian Integrasi Numerik

  
  

  • 

    8.1 Metode Trapesium Page

    Bentuk trapesium akan semakin didekati apabila jumlah titik semakin banyak oleh karena sisi yang sepanjang kurva semakin cenderung ke bentuk garis lurus. Aar tidak bingung, silahkan klik 8.1 Metode Trapesium.
    

  • 

    8.2 Metode Simpson Page

    Metode ini adalah dengan menggantikan antara xi-1 dan xi+1 dengan fungsi busur parabola melalui fi-1, fi, fi+1. Selengkapnya silahkan klik 8.2 Metode Simpson.

  • 

    8.3 Metode Nilai Rata-rata Page

    Suatu fungsi yang kontinu dalam interval [a,b] akan ada nilai rata-rata dari fungsi tersebut, selanjutnya silahkan klik 8.3 Metode Nilai Rata-rata.

  • 

    PPT BAB 8 Penyelesaian Integrasi Numerik File

    Silahkan download PPT BAB 8 disini, dan jangan lupa belajar

  • 

    Tugas BAB 8 Penyelesaian Integrasi Numerik Assignment

    Materi sudah dipelajari, saatnya penugasan ya. Kalian dapat mengupload hasil tugas kalian Tugas BAB 8 Penyelesaian Integrasi Numerik.

  • 

    Forum Diskusi BAB 8 Penyelesaian Integrasi Numerik

    Jika ada yang ingin kalian tanyakan terkait metode-metode pada penyelesaian integrasi numerik, silahkan klik disini.

• BAB 9 PENYELESAIAN PERSAMAAN DIFERENSIAL PARSIAL

  
  

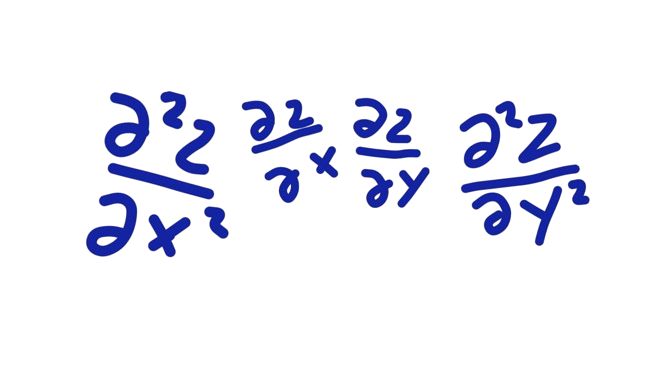
  Ini adalah BAB terakhir yang akan kita pelajari yaitu tentang persamaan differensial parsial, ada 3 jenis persamaan yang akan kita pelajari yaitu persamaan parabol, ellips, dan hyperbol. Selengkapnya bisa simak video penjelasan dan klik sub bab-sub bab berikut ini ya.

  
  

  
  

  Video Penjelasan Penyelesaian Persamaan Diferensial Parsial

  • 

    9.1 Jenis Persamaan Page

    Ada beberapa macam dalam persamaan diferensial, klik 9.1 Jenis Persamaan untuk materi selengkapnya ya

  • 

    9.2 Persamaan Parabol Page

    Persamaan ini ditemui pada masalah difusi pada keadaan transien, selengkapnya bisa klik 9.2 Persamaan Parabol.

  • 

    9.3 Persamaan Ellips Page

    Persamaan ellips contohnya adalah persamaan Laplace dengan aplikasi seperti pada persamaan garis aliran, persamaan difusi, persamaan perpindahan panas regim permanen, persamaan perpindahan masa. Untuk bentuk persamaan ellips bisa klik 9.3 Persamaan Ellips.
    

  • 

    9.4 Persamaan Hyperbol Page

    Silahkan klik 9.1 Persamaan Hyperbol untuk melihat contoh-contoh persamaan hyperbol.

  • 

    PPT BAB 9 Penyelesaian Persamaan Diffreensial Parsial File

    Silahkan klik PPT BAB 9 Penyelesaian Persamaan Diffreensial Parsial untuk mendownload materinya ya
    

  • 

    Tugas BAB 9 Penyelesaian Persamaan Differensial Parsial Assignment

    File ini berisikan tugas BAB 9, silahkan dikerjakan dan jangan lupa diupload tepat waktu ya.. Silahkan download disini.

  • 

    Forum Diskusi BAB 9 Penyelesaian Persamaan Differensial Biasa

    Jika ada yang ingin ditanyakan terkait BAB 9 mengenai jenis-jenis persamaan, silahkan klik disini

• UAS (Ujian Akhir Semester)

  

  Assalamualaikum wr wb.. Salam hangat, semua materi telah kita pelajari dan kali ini kita memasuki Ujian Akhir Semester. Berikut merupakan link untuk mendownload Form Laporan dengan cara klik Form Laporan Proyek. Ketentuan Proyek: 1) Buatlah kelompok dengan jumlah maksimal 4 mahasiswa, 2) Tentukan nama kelompok sesuai musyawarah bersama, 3) isi Form Laporan Proyek yang telah disediakan dan permintaan tiap demi tahap, 4) pilih topik yang sesuai dengan materi yang telah diberikan, 5) setelah mengisi silahkan upload laporan pada tempat yang telah disediakan dan pastikan tidak terlambat saat mengupload ya.

  Untuk mengupload laporan proyek komputasi numerik, kami sediakan link dibawah ya. Dan di akhir perkuliahan ini saya meminta maaf jika ada salah dan kurang. Terimakasih untuk mahasiswa yang telah mengikuti mata kuliah ini, semoga bermanfaat dan mendapatkan nilai yang sesuai dengan yang diharapkan.. Semangat terus ya. 

  • 

    Unggah file laporan projek disini Assignment

    Silahkan unggah laporan projek di link berikut: unggah laporan projek komputasi numerik. Pengumpulan tugas projek paling lambat hari Rabu tanggal 31 Desember 2024 pukul 23.59 dalam format pdf. Ketua saja yang menggunggah laporannya.. terimakasih semua

  • 

    Forum Diskusi UAS

    Silahkan klik disini jika ingin berdiskusi terkait soal UAS, penilaian dan lainnya..

• EVALUASI PERKULIAHAN

  Assalamualaikum wr wb semua...tiba saatnya untuk mengisi kuisioner terkait perlaksanaan perkuliahan. Silahkan klik link: isi kuisioner untuk mengisinya atau klik logo di bawah ini. Terimakasih atas kerjasamanya. Salam semangat.

  • 

    Angket Respon Mahasiswa Terhadap Model Pembelajaran Project Based Learning Feedback

• PENUTUP

  
  

  Hallo semuanya, tiba di akhir perkuliahan ya.. Semua materi yang terdiri dari 9 bab telah kita pelajari, kita juga sudah melakukan evaluasi. Semoga nilai yang didapat adalah nilai terbaik, saya mengucapkan terimakasih banyak atas antusias dalam mengikuti mata kuliah ini dan mohon maaf atas segala kurang dan salah.. Perkuliahan ini saya akhiri, wassalamualaikum wr wb. SEE YOU ON TOP yaa